Using Sympy for Analytical Maths

This is an example of how i would use sympy to evaluate a set of analytical questions, for example:

Find $\forall a \in [0,12,24,30,99]$ and $b=100$:

$$ \int_a^b \frac{\alpha x^{3} - \sin(2x)}{\sqrt{\beta e^x}} dx $$

Where $\alpha = 2.341$, $\beta = e^x$

First we need to import the library (and start the printing for nice easy to read stuff):

1
2
3
import sympy as sp

sp.init_printing()

Now create the eqn above so we can evaluate it

1
2
3
a, b, alpha, beta, x = sp.symbols('a b \\alpha \\beta x')
expr = (alpha * x ** 3 - sp.sin(2 * x)) * (1 / sp.sqrt(beta * sp.E ** x))
expr

$$ \frac{1}{\sqrt{\beta e^{x}}} \left(\alpha x^{3} - \sin{\left (2 x \right )}\right) $$

This like the integrand we hav above. Now theres a few things we can do, if we know $\alpha$ and $\beta$, which we do, we can sub them in. then we will have a more simple expression:

1
2
expr2 = expr.subs({alpha: 2.341, beta: sp.E ** x})
expr2

$$ \frac{1}{\sqrt{e^{2 x}}} \left(2.341 x^{3} - \sin{\left (2 x \right )}\right) $$

If we wanted we could now evaluate this using the .subs() command again (this time with a value for x such as .subs(x,3)), but we're asked to evalue the integral:

1
2
integral = sp.integrate(expr2, (x, a, b))
integral

$$ \frac{2.341 a^{3}}{\sqrt{e^{2 a}}} + \frac{7.023 a^{2}}{\sqrt{e^{2 a}}} + \frac{14.046 a}{\sqrt{e^{2 a}}} - \frac{2.341 b^{3}}{\sqrt{e^{2 b}}} - \frac{7.023 b^{2}}{\sqrt{e^{2 b}}} - \frac{14.046 b}{\sqrt{e^{2 b}}} + \frac{0.2}{\sqrt{e^{2 b}}} \sin{\left (2 b \right )} + \frac{0.4}{\sqrt{e^{2 b}}} \cos{\left (2 b \right )} - \frac{14.046}{\sqrt{e^{2 b}}} - \frac{0.2}{\sqrt{e^{2 a}}} \sin{\left (2 a \right )} - \frac{0.4}{\sqrt{e^{2 a}}} \cos{\left (2 a \right )} + \frac{14.046}{\sqrt{e^{2 a}}} $$

Now we need to calculate all the values of this expression for every combination of $a \in [0,12,24,30,99]$ and $b=100$. We can do this by starting with lambdifying the expression into a callable function:

1
2
my_callable = sp.lambdify((a, b), integral)
my_callable(1, 2)  # this will sub in a=1 and b=2 to the above.

$$ 1.6786017689393038 $$

Now we just loop over the varable s for a and we can print out the values:

1
2
3
4
for a in [0, 12, 24, 30, 99]:
    print("a =", a)
    print(my_callable(a, 100))
    print()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
a = 0
13.645999999999999

a = 12
0.03219056961943131

a = 24
1.3876938438535285e-06

a = 30
6.546926902186657e-09

a = 99
1.470461229758446e-37

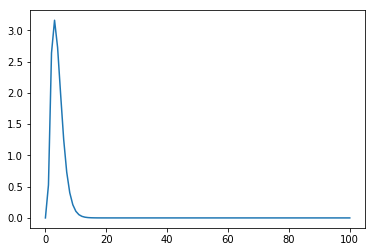
This decreasing sequence is expected as were taking essentially taking area slices of the below plot, moving further left each time as a starting point.

1
2
3
4
5
6
%matplotlib inline
import matplotlib.pyplot as plt

X = [x for x in range(0, 101)]
expr2_callable = sp.lambdify(x, expr2)
plt.plot(X, [expr2_callable(x) for in_x in X])

1
[<matplotlib.lines.Line2D at 0x24a166e8668>]

And we're done!