Taylor Expansions in PDEs

Ever wondered what the uses for taylor expansions are in the field of differential equations? no? well you should, its rather facinating...

First, what is a taylor expansion? well, basically, it says if youre trying to evaluate a function at a point that's "close enough" to a point you already know you'll be able to represent this slight difference as an infinate series:

$$ (1)\quad f(x+h)=f(x)+hf'(x)+\frac{h^2}{2!}f''(x)+O(h^3) $$ Or if you're more comfortable with summation notation: $$ (2)\quad f(x+h)=\sum^{\infty}_{n=0}\frac{(h)^n}{n!}f^{(n)}(x) $$

Here $O(h^3)$ represents an arbitrary function of order $h^3$ (basically just a function in $h$ with the smallest $h$ term being $h^3$, this is important and we will use this in a bit...

So how does this relate to a PDE? Well, we can estemate derivatives of a functon using this method, right? (as long as everything is nicly behaved) take eqn (1) above, and rearange it,get fid of a few terms & this will give you:

$$ (3)\quad f'(x)=\frac{f(x+h)-f(x)}{h}-\frac{h}{2!}f''(x)+O(h^2) $$ or setting $F'(x)\approx f'(x)$ $$ (4)\quad F'(x)=\frac{f(x+h)-f(x)}{h} $$

From here we can see that we can somewhat accuratly calculate a derivative of a function using the evaluation at 2 points that are "close enough" together (this can be done in both directions by using $-h$ insted). That's cool, but now what?

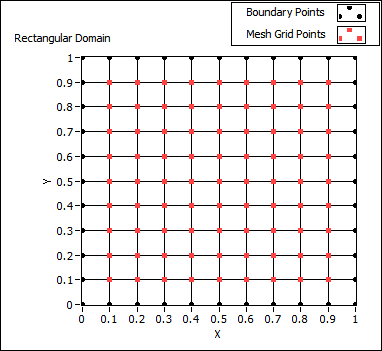
See this grid? This is a plane where a PDE lives. We can solve the PDE at a point on this plane if we use the above fomulas in a clever way. Imagine were ust working on the line $y=0$ and we want to work out $f'(0.3)$ where $f(x)=x^2$, how do we do this?

1. Remember that we can aprox $f'(x)$ using (4).
2. Set $h$ to be 0.1, or the spacing between the grid points.
3. Then we get $$ F'(0.3)=\frac{f(0.3+0.1)-f(0.3)}{0.1} $$
4. Which we get $f'(0.3)\approx F'(0.3)=\frac{(0.4)^2-(0.3)^2}{0.1}= 0.7 \approx 2(0.3)$
5. And we have our approxamate answer at $x=0.3$

We can even make this more accurate by taking our expansion in $+h$ and finding the difference from our expansion in $-h$. essentially taking the difference between the 2 points either side of the position, $x$, we're looking at. we get:

Forward: $f(x+h)=f(x)+hf'(x)+\frac{h^2}{2!}f''(x)+O(h^3)$

Backward: $f(x-h)=f(x)-hf'(x)+\frac{(-h)^2}{2!}f''(x)+O(h^3)$

so we can take the difference:

$$ f(x+h)-f(x-h)=+2hf'(x)+O(h^3) $$

$$ \Rightarrow f'(x)=\frac{f(x+h)-f(x-h)}{2h}+O(h^2) $$

or setting $F'(x)\approx f'(x)$

$$ (5)\quad F'(x)=\frac{f(x+h)-f(x-h)}{2h} $$

Its a much nicer result beacuse our $O(h^2)$ term well decay faster if we make the difference, $h \rightarrow 0$. We can show that the error we get is much smaller if we try again, so lets do the exaple of $f'(0.3)$ where $f(x)=x^2$ again:

1. With $F'(x)\approx f'(x)$ we can use eqn (5).
2. Subbing everything in we get $F'(0.3)=\frac{f(0.3+0.1)-f(0.3-0.1)}{2(0.1)}=\frac{(0.4)^2-(0.2)^2}{0.2}=0.6$
3. TADAAA

Using this 2 sided approach is called the centered difference approximation and is much more accurate, it should be used if possible. Hint: if youre trying to calculate approx for $f'(x)$ and $f(x\pm h)$ doesn't exist, then a problem has been encoutered and must be solved. There are ways of solving these we will come on to.

But first I hear you ask "Toby, is there a way of doing this for approximating a second derivative?" to which I reply: "why yes, its easy enough, just rearange the taylor expansion for the particular derivative you need!". I have lied to you though, it is not "easy enough"; with a simple push however it can be.So what are we really looking for? We want to find this approximation to the second derivative, or $F''(x)\approx f''(x)$. And we want this $F(x)$ as a linear combination of the points $f(x-h),\ f(x),\ f(x+h)$ or, in a more verbose defintion:

$$ F''(x)=Af(x-h) + Bf(x) + Cf(x+h) $$ which then gives, after expanding these points out, or using both the forward and backwards expansions given above: $F''(x)=A\large{[} f(x) + hf'(x) + \frac{h^2}{2!} f''(x) + O(h^3) \large{]}$ $\qquad \quad +B,f(x)$ $\qquad \quad +C\large{[} f(x) - hf'(x) + \frac{(-h)^2}{2!} f''(x) + O(h^3) \large{]}$

Where collecting terms in this expansion provides a nice set of coefficents to solve for: $$ F''(x)=[A+B+C], f(x)+h[A-C], f'(x)+\frac{h^2}{2!}[A+C], f''(x)+[A+C], O(h^3) $$

We want to set $(A+B+C)=0$ , $(A-C)=0$ and $\frac{h^2}{2!}[A+C]=1$ then the rest of the combos make up the error, so they can be ignored. Solving all of these we can just set:

• $A = C = \frac{1}{h^2}$ by the second two eqns.
• $B = -(A+B) = -\frac{2}{h^2}$ by the first.

These coeficients allow the approximation for $f''(x) \approx F''(x)$ to be: $$ F''(x)=Af(x-h) + Bf(x) +Cf(x+h)=\frac{f(x-h) - 2f(x) +f(x+h)}{h^2} $$

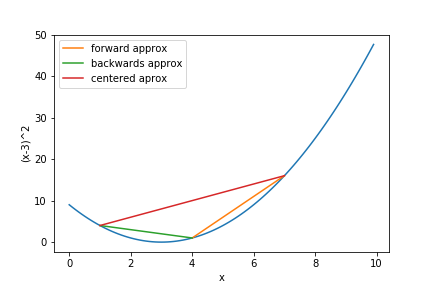
The motive for taking centered approximations can be seen below. Its obvious the red line has a gradient closer to $f(4)$ than the other two lines.

From this point on we can increase the dimension of $f(x)$ to be a function of 2 variables: $f(x,y)$, and we can expand $f$ in both $x$ (as we did before), and $y$ (by using the spacing of $\pm k$ insted of $\pm h$). Then we can calculate partial differentials in the same manner; expand the taylor series and rearange for an approximation. Only this time insted of arbitary spacing we use the concept of creating a mesh with points spaced out over our domain this is known asdiscritizing the domain(the grid above is a prime example). This then gives:

$$ f(x\pm h,y) = f(x,y) \pm h \frac{\partial f(x,y)}{\partial x} + \frac{h^2}{2!} \frac{\partial^2 f(x,y)}{\partial x^2} + O(h^3) $$ and $$ f(x,y \pm k) = f(x,y) \pm k \frac{\partial f(x,y)}{\partial y} + \frac{k^2}{2!} \frac{\partial^2 f(x,y)}{\partial k^2} + O(k^3) $$

Note that the partial differentials have are actually evluated at a given $x$ and $y$ so it may be more obvious whats going on using: $\frac{\partial f(x,y)}{\partial x} = \frac{\partial f}{\partial y}\mid_{x,y}$