The Data Compression course covers a variety of compression techniques that must be learned. Some are simple, and some are complicated, but all are not as hard as learning how computers actually work.

Lossless Techniques

Shannon Coding

Possibly the simplest, this is purely for research and isnt really used anywhere. We will start with the following properties:

$$ A={x_1,\ x_2,\ x_3} $$ $$ P={\frac{1}{2},\frac{3}{8},\frac{1}{8}} $$

Now we start the steps:

1. Using the probabilities in $P$ create the cumulative probabilities list $P_C$, starting at $0$: $$ P_C={0,\frac{1}{2},\frac{7}{8}}={0,\ 0.5,\ 0.875} $$ This will be used, once converted to binary, to be a the representations of our words. This will require us to know how many bits of the binary form to include however, that is step 2.
2. To find the number of bits each word requires we need to find the self-information of the word. This is done using the self-information function: $$ I(a_i) = \lceil-log_2(p_i)\rceil $$ This gives: $$ I(A)={1,2,3} $$ Which represents the lengths of each of the expansions for the probabilities found in step 1.
3. Now we can convert $P_C$ to binary up to the length given in $I(A)$, this can be done any way you want. I use the multiplying expansion technique (not shown). This gives:

$$ 0\rightarrow 0\quad | \quad 0.5\rightarrow 10,\quad | \quad 0.875\rightarrow 111 $$

These are the expansions for the respective codewords: $$ x_1=0\quad | \quad x_2=10,\quad | \quad x_3=111 $$ This gives a uniquely decodable prefix code but it may not be optimal, the average compression length is: $$ L_{avg}=\sum^{|A|}_{i=1} l_i p_i = (1\cdot \frac{1}{2})+(2\cdot \frac{3}{8})+(2\cdot \frac{1}{8}) = \frac{13}{8} = 1.625 $$

Shannon-Fano Coding

Shannon-Fano coding is very hard to describe mathematically, It leverages the property that binary trees will create prefix codes if the leaves represent words. we will start with a longer code alphabet than before: $$ A={a,\ b,\ c,\ d,\ e,\ f} $$ $$ P={0.05,\ 0.1,\ 0.12,\ 0.13,\ 0.17,\ 0.43} $$

1. The first step is to sort the alphabet by the probabilities: $$ A={f,\ e,\ d,\ c,\ b,\ a s} $$ $$ P={0.43,\ 0.17,\ 0.13,\ 0.12,\ 0.1,\ 0.05 } $$
2. Now the probabilities are sorted, make this the "root" of the tree, then split the list in half by weighting the probabilities so they're equal on both sides. Now append 0 to the left groups members, and 1 to the right. $$ 0:[f:0.43,e:0.17]\ |\ 1:[d:0.13,c:0.12,b:0.1,a:0.05] $$
3. Repeat step 2 for each of the groups in until you get groups of order 1, this is essentially constructing a tree: $$ 00:[f:0.43] |\ 01:[e:0.17]\ |\ 10:[d:0.13,c:0.12]\ |\ 11:[b:0.1,a:0.05] $$ $$ 00:[f:0.43]\ |\ 01:[e:0.17]\ |\ 100:[d:0.13]\ |\ 101:[c:0.12]\ |\ 110:[b:0.1]\ |\ 111:[a:0.05] $$ or, as a tree:

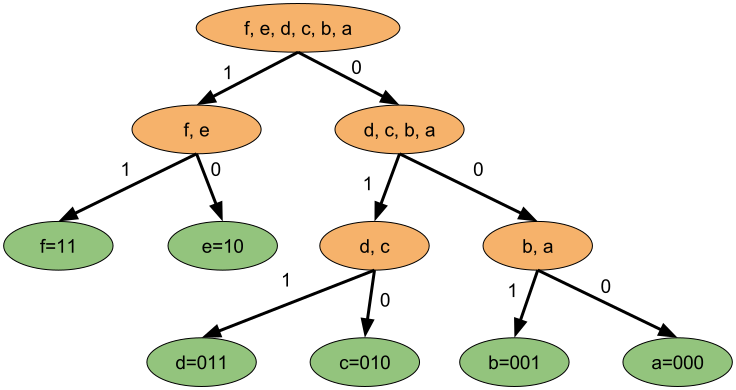
This gives a uniquely decodable prefix code but it may not be optimal, the average compression length is: $$ L_{avg}=\sum^{|A|}_{i=1} l_i p_i = (2\cdot 0.43)+(2\cdot 0.17)+(3\cdot 0.13)+(3\cdot 0.12)+(3\cdot 0.1)+(3\cdot 0.05)= 2.4 $$

Hufman Coding

Hufman coding will always give an optimal tree, but again is hard to describe mathematically. It uses forrests of nodes that are joined in certain orders to create a tree the same as Shanon-Fano coding. We will use the same code as in the Shanon-Fano example: $$ A={a,\ b,\ c,\ d,\ e,\ f} $$ $$ P={0.05,\ 0.1,\ 0.12,\ 0.13,\ 0.17,\ 0.43} $$

1. A node has 2 properties; the contained elements & the cumulative probability of the elemens in the node. For all elements in the alphabet, create a node: $$ (a,\ 0.05)\quad (b,\ 0.1)\quad (c,\ 0.12)\quad (d,\ 0.13)\quad (e,\ 0.17)\quad (f,\ 0.43) $$
2. Create a single new node, this is the parent of the 2 nodes in your set with the lowest cumulative probabilities: $$ (ab:(a,\ 0.05)\ (b,\ 0.1),0.15)\quad (c,\ 0.12)\quad (d,\ 0.13)\quad (e,\ 0.17)\quad (f,\ 0.43) $$
3. Repeat step 2 over and over until you have a tree: $$ (ab:(a,\ 0.05)\ (b,\ 0.1),0.15)\quad (cd:(c,\ 0.12)\ (d,\ 0.13),0.25)\quad (e,\ 0.17)\quad (f,\ 0.43) $$ $$ (abe:(ab:(a,\ 0.05)\ (b,\ 0.1),0.15)\ (e,\ 0.17),0.32)\quad (cd:(c,\ 0.12)\ (d,\ 0.13),0.25)\quad \quad (f,\ 0.43) $$ $$ \ldots $$
4. add numbers to the tree branches and append these numbers until reaching a node. these are the codewords.

It is easier to see as a gif:

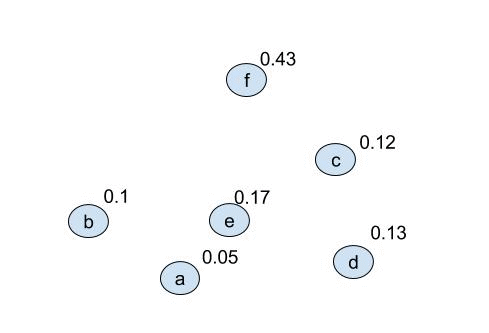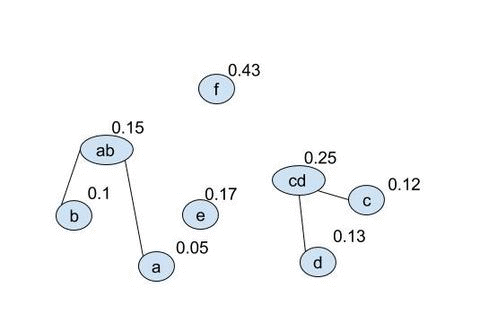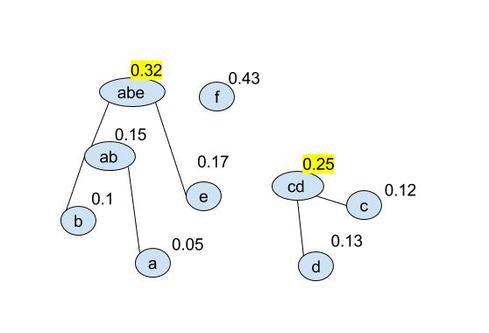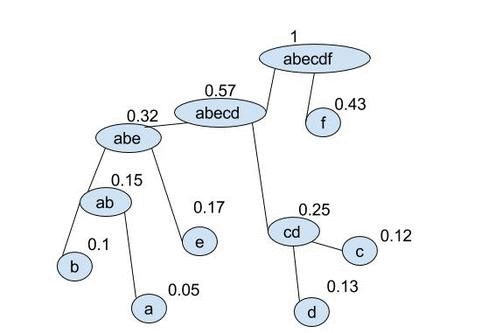
once the final tree is given numbers can be applied to the vertacies and the codewords found. Because of the optional 0-1 choice this will not produce unique codes. We can produce the following coded alphabet: $$ a=0101,\ b=0100,\ c=001,\ d=000,\ e=011,\ f=1 $$ (it can be seen by replacing 1s with 0s in the above that this is non unique). This wll also produce an optimal code: $$ L_{avg}=\sum^{|A|}_{i=1} l_i p_i = (4\cdot 0.05)+(4\cdot 0.1)+(3\cdot 0.12)+(3\cdot 0.13)+(3\cdot 0.17)+(1\cdot 0.43) = 2.29 $$